A while back I needed a logical formalism with clear semantics for KB updates that was non-monotonic and had an all-or-nothing flavor, i.e., either all updates are applied or none of them.
I start by elaborating on the use case that triggered my need for this. If you’re only interested in the continuous-transaction concept, feel free to skip ahead.
Use case
The use case involved the integration of comorbid Clinical Practice Guidelines (CPG). In general, CPG are carefully crafted, evidence-based recommendations for guiding diagnosis, prognosis, and treatment of a specific illness [1]. By computerizing CPG using e.g., PROforma [2] or SDA* [3], Clinical Decision Support (CDS) systems are able to deliver care recommendations based on the latest patient medical data.
In case of comorbidity however, i.e., a patient suffering from multiple conditions at the same time (e.g., hypertension and diabetes), the relevant CPG sometimes contain adverse interactions. For instance, hypertension guidelines recommend thiazide diuretics but these often worsen glycemic control in diabetes patients. Aligning multiple CPG to avoid adverse interactions, and, ideally, improve quality of life and optimize resources , is typically called the integration / alignment / mitigation of comorbid CPG.
In our work, we wanted to focus on execution-time integration of comorbid CIG—since many relevant factors only become known at execution-time. Most importantly, these factors include the patient’s changing health parameters, but also the availability of clinical resources, and so on.
For instance, guidelines for Venous Thromboembolism (VTE) prescribes treatment with Warfarin, whereas antibiotics (e.g., Erythromycin) are recommended for Respiratory Tract
Infection (RTI). VTE and RTI often occur comorbidly, but Erythromycin potentiates the anticoagulant effect of Warfarin, thus increasing the risk of bleeding. However, simply stopping treatment with either medication is not an option, since both are needed to treat the respective conditions. Clinical pragmatics would rather dictate reducing the Warfarin dose while Erythromycin is being prescribed, based on the patient’s INR value, until it returns to normal.
We can express this as follows:
:Warfarin_Erythromycin a :EventBasedReplacePolicy ;
:intPt cig:prescribe_Warfarin ;
:event cig:prescribe_Erythromycin ;
:replacement [ :time :during ;
:value cig:adjust_Warfarin_during_Erythromycin ;
:exitCond [ cig:INR_value cig:normal ] ] ;
:replacement [ :time :after ;
:value cig:adjust_Warfarin_after_Erythromycin ;
:exitCond [ cig:INR_value cig:normal ] ] .The prescription of Warfarin is an integration point, and the prescription of Erythromycin is the event: (a) during the event, the Warfarin dose (integration point) will be adjusted based on the patient’s INR value, until the value returns to normal; (b) after the event (i.e., Erythromycin treatment), the Warfarin dose (integration point) will again be adjusted until the INR value becomes normal.
To support these kinds of scenarios, using a “regular” set of rules, i.e., without semantics for change and lacking an all-or-nothing flavor, one would need (a) a set of rules to apply the “during” and “after” replacements, which infer actions to adjust Warfarin prescription; and (b) a set of rules to undo these replacements, i.e., inferring actions to undo the adjustment when the event is no longer active, or the INR values return to normal.
This is only one example of an integration policy; there were many more, some involving not only replacements but also “delay” operations. This lead to a very complex, unwieldy and difficult to maintain ruleset, which you can find in our journal paper [4] in quite some (excruciating) detail.
Transaction Logic
Transaction Logic ($\mathcal{Tr}$) is a non-monotonic logic with clear semantics for changes in a knowledge base (KB), where a rule has an all-or-nothing flavour, i.e., either all its updates are applied, or none of them are, meaning they can be considered as atomic transactions.
$\mathcal{Tr}$ relies on executional entailment, where establishing the truth value of an expression involves executing that expression. In particular, proving a query involves finding an execution path that entails the query:
$$P, D_0, .., D_n \models \psi$$
Where P represents a transaction base, is an execution path, and ψ is a transaction. In particular, the entailment states that transaction ψ is entailed by execution path $D_0, .., D_n$ given P . For example, the following holds:
$$P, D, D+\{in(pie, sky)\} \models ins:in(pie, sky)$$
If update (or “transition”) $ins:in(pie, sky)$ is defined as inserting the atom $in(pie, sky)$.
Transaction Logic defines special semantics for logical conjunction, disjunction and negation, and introduces a new operator called serial conjunction (symbol ). We only utilize serial conjunction here. The following executional entailment:
$$P, D_0, .., D_n \models \psi \otimes \phi$$
Will hold if and only if an execution path exists where the following holds: $D_0, .., D_k \models \psi$ and $D_k, .., D_n \models \phi$. For instance, the following entailment holds:
$$P, D, D+\{lost\}, D+\{lost, sad\} \models ins:lost \otimes ins:sad$$
If transitions ins:lost and ins:sad are defined to insert atoms lost and sad into the KB, respectively.
Using serial conjunction, $\mathcal{Tr}$ allows combining updates with conditions. This means that pre- and post-conditions for updates are possible. For example, transaction $ins:won \otimes happy$ includes an update followed by a condition: in case “happy” is true in the final KB state, then the transaction will be committed; else, the transaction will be rolled back to the initial state.
This notion of a post-condition makes $\mathcal{Tr}$ interesting for many practical applications. For example, in case an update can be linked to an external component (anything from a planning algorithm to a robot), it may turn out to be unsuccessful. In that case, any prior update in the transaction will be rolled back.
Rules are written in the form of $p := \phi$, where $\phi$ is any formula and p is an atomic formula. This rule has a procedural interpretation: to prove p it is sufficient to prove $\phi$, which, in line with executional entailment, involves executing $\phi$. For example:
$deposit(acc, amt) := balance(bal,acc) \otimes del:balance(bal, acc) $
$\otimes ins:balance(bal+amt,acc) \\ \otimes balance(bal2,acct) \otimes bal2=bal+amt$
In case the post-condition $bal2=bal+amt$ does not hold, the deposit transaction will be rolled back. We refer to Bonner and Kifer [5] for much more on $\mathcal{Tr}$.
Continuous Transactions?
For instance, by using these kinds of transactions to implement the CIG integration scenario, we no longer need (a) a separate ruleset to apply “during” and “after” replacements, and (b) a second ruleset to undo these replacements (i.e., when conditions no longer hold). Instead, we can simply have transactions that apply a during / after replacement – when conditions no longer hold, the replacements will be rolled back by design. This may not seem like such a big deal, but really, have a look at the journal paper [4] and you’ll see how unwieldy a non-transactional ruleset can quickly become in the context of CIG integration. (I’m not saying this to bash the authors of this paper – I’m one of the authors and was partly responsible for the ruleset.)
However, transactions in are rather considered subroutines: invoking a query such as $?- deposit(P, U)$ will attempt to execute the rule body of the deposit transaction, as per executional entailment. In dynamic scenarios, a condition may become false, or true, at any time after its initial execution. For instance, at runtime, an external planner may decide that a given constraint is no longer feasible, or, inversely, a constraint suddenly becomes feasible. At that point, the transaction should also be rolled back or re-applied, respectively.
Essentially, this requires us to keep track of successful execution paths, so they can be rolled back at any time later on. The RETE forward-chaining algorithm keeps successful joins by design, which collectively can be seen as “execution paths”. This makes RETE an straightforward choice for implementing “continuous” transactions. You can find the implementation as an extension of Apache Jena on GitHub. I’m currently preparing a publication on this topic so I will just give a broad-brush overview here and leave the details to that paper.
In a nutshell, the RETE algorithm compiles a RETE structure for a given rule. So-called alpha nodes represent clauses within the rule, and beta nodes represent joins within the rule. An alpha node has an alpha memory that keeps tokens matched to the clause; a beta node has a beta memory that keeps tokens that were successfully joined up until that point.The RETE structure for an example rule is shown below (example taken from Van Woensel et al. [6]):
Rule: $(?c,intersectionOf,?x),(?x,hasMember,?ci),(?y,type,?c) → (?y,type,?ci)$
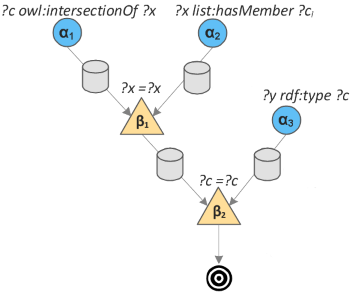
The $\beta_1$ node will keep all tokens that were successfully joined on the $?x$ variable; the $\beta_2$ node will keep all tokens that were previously joined on the $?x$ variable and successfully joined on the $?c$ variable. By keeping intermediate join results, a lot of join work can be avoided. For our purposes, these collective join results constitute prior execution paths, which allows us to easily rollback prior executions of a rule at runtime.
Adapted RETE algorithm
To support continuous transactions, we adapt the standard RETE algorithm as follows.
– Each alpha node can represent a functor (or built-in) that involves issuing an update to the KB. When rolling back a transaction, alpha nodes will be notified in order to rollback their update.
– The join process is extended as follows.
(1) When joining an incoming token fails, a rollback is initiated .
Due to the nature of the RETE algorithm, we know that all prior nodes contributed to this join. Hence, this rollback will propagate back to the start of the RETE structure.
Essentially, this supports the “classic” $\mathcal{Tr}$ where, during a single rule execution, an update fails and the prior updates need to be rolled back.
(2) When a deleted token is successfully joined, a rollback is initiated.
This supports the “continuous” $\mathcal{Tr}$ where a transaction can be rolled back at any point during runtime.
In this case, the rollback will proceed in both directions of the RETE structure:
Prior nodes : as before, due to the nature of the RETE algorithm, we know that all prior nodes contributed to this join. Hence, this rollback will propagate back to the start of the RETE structure.
Next nodes : by design, the RETE algorithm will propagate the token deletion down the RETE structure (since all tokens resulting from a join with this deleted token should be deleted as well). Whenever this deleted token is successfully joined to a beta node, we will issue a rollback to the connected alpha node.
For the concrete implementation, please refer to the GitHub repository.
References
[1] Brush, J.E., Radford, M.J., Krumholz, H.M.: Integrating Clinical Practice Guidelines Into the Routine of Everyday Practice. Crit. Pathways Cardiol. A J. Evidence-Based Med. 4, 161–167 (2005).
[2] Sutton, D.R., Fox, J.: The syntax and semantics of the PROforma guideline modeling language. J Am Med Inf. Assoc. 10, 433–443 (2003).
[3] Riano, D.: The SDA Model: A Set Theory Approach. Twentieth IEEE International Symposium on Computer-Based Medical Systems (CBMS’07). pp. 563–568. IEEE (2007).
[4] Jafarpour, B., Abidi, S.S.R., Abidi, S.R.: Exploiting Semantic Web Technologies to Develop OWL-Based Clinical Practice Guideline Execution Engines. IEEE J. Biomed. Heal. Informatics. 20, 388–398 (2016).
[5] Bonner, A.J., Kifer, M.: An Overview of Transaction Logic. Theor. Comput. Sci. 133, 205–265 (1994).
[6] Van Woensel W., Abidi S.S.R. (2018) Optimizing Semantic Reasoning on Memory-Constrained Platforms Using the RETE Algorithm. In: Gangemi A. et al. (eds) The Semantic Web. ESWC 2018. Lecture Notes in Computer Science, vol 10843. Springer, Cham
